Una meridiana solar es un instrumento gnomónico que nos indica, sobre una línea, el momento del paso del Sol por el meridiano del lugar, el mediodía solar, cada uno de los días del año.
 |
| Esquema de la meridiana de San Petronio en Bolonia |
La construcción de meridianas ya era conocida en la época del arquitecto Marco Vitrubio, siglo I a. C. que lo describe en el libro IX de su obra De Architectura , tratado más antiguo de arquitectura que ha llegado hasta nuestro tiempo.
Fue a partir de finales del siglo XV cuando, una vez perfeccionados los métodos y cálculos, cuando se construyeron las más grandiosas y elegantes meridianas que aún podemos admirar en la actualidad.
Para su construcción se realizaba un orificio en la parte superior de un muro, orientado al sur, de altos edificios ( iglesias, palacios,…) de manera que, al mediodía solar, el rayo de sol que incide en él se refleja sobre un segmento trazado en el suelo del edificio.
Ese segmento será de mayor longitud cuanto mayor sea la altura donde esté situado el orificio.
Ese punto luminoso reflejado cada día, a mediodía, sobre la meridiana en el suelo, describe a lo largo de un año una curva en forma de ocho llamada analema.
En los solsticios, donde la altura del sol respecto al plano ecuatorial de la tierra es la mayor y la menor, ese punto luminoso se encuentra en los extremos del segmento.
El resto de los días, dependiendo de la altura del sol en ese día, el punto luminoso se alejará o acercará del segmento pero siempre describiendo una trayectoria de un ocho (8).
En la siguiente imagen vemos la fachada del Hotel Royal Victoria en Pisa con una pequeña meridiana que hemos ampliado para que se vea el orificio por donde entra el rayo de sol a mediodía y la curva que describe, en forma de analema, con los meses del año.
En la siguiente imagen vemos la fachada del Hotel Royal Victoria en Pisa con una pequeña meridiana que hemos ampliado para que se vea el orificio por donde entra el rayo de sol a mediodía y la curva que describe, en forma de analema, con los meses del año.
 |
| Analema en la fachada del Hotel Royal Victoria de Pisa |
Las meridianas se utilizaban para realizar cálculos astronómicos, calcular la duración del año solar, saber cuando comenzaban y cuánto duraban las estaciones, conocer el ángulo de declinación,…
Meridianas más importantes:
Entre las meridianas más importantes que podemos admirar y que se consideran verdaderas obras de arte y de ciencia destacaremos las siguientes:
I.- En 1437 el matemático y astrónomo Ulugh Beg (1393-1449), parece ser, que utilizó una meridiana en Santa Sofía de Estambul, con una longitud de 50 m. para calcular la duración del año sidéreo, el resultado que obtuvo fue de que un año tiene 365,2570370… días
II.- En 1475 Paolo dal Pozzo Toscanelli (1397-1482) construye una
meridiana en Santa María de Fiore , en Florencia y coloca el broncino con el orificio por donde entra el sol a unos 90 metros de altura, que es la mayor altura a la que se ha colocado este orificio.
 |
| Meridiana de Sta. Mª de Fiore |
En el siguiente enlace, podemos consultar, en este blog, el artículo escrito sobre Toscanelli , en el que además podemos visionar dos vídeos con el efecto que produce el sol sobre esta meridiana.
III.- También en Florencia, en la iglesia de Santa María Novella, podemos contemplar otra meridiana de 21,35 metros de longitud, construida por Ignazio Danti (1536-1586), matemático que utilizó la iglesia como un laboratorio para las investigaciones astronómicas, en su fachada construyó un reloj solar de múltiples horas y una esfera armilar.
IV.- Más de siglo y medio después de la de Santa Mª de Fiore , el astrónomo Giovanni Doménico Cassini (1625-1712) construyó, en 1655, la línea meridiana de la iglesia de San Petronio de Bolonia sobre una anterior de Ignazio Danti destruida al ampliar el templo.
 |
| Meridiana de San Petronio (en rojo) |
Tiene el orificio a 27 metros de altura y la longitud de la línea con sus 66,7 metros es de las de mayor longitud construida.
La meridiana cubre más de la mitad de la iglesia (como se observa en la imagen de la planta de la iglesia de la derecha en rojo ) y sigue funcionando con perfectamente en la actualidad
V.- En 1786 se construyó la meridiana del Duomo de Milán.
 |
| Meridiana del Duomo de Milán. |
VI.- En Roma, vamos a citar tres:
Una en la Salla della Meridiana en la Torre de los Vientos del Vaticano , actual observatorio astronómico (Specula Vaticana) construida por de Ignazio Danti (1536-1586).
 |
| Salla della Meridiana en la Torre de los Vientos (Specula Vaticana) |
Y otra en la basílica de Santa Mª degli Angeli e dei Martiri, de 20 metros, realizada en 1702 por Francesco Bianchini (1662-1729) considerada como una de las más bellas.
 |
| Meridiana de Santa María degli Angeli e dei Martiri |
Una tercera meridiana podemos encontrarla en la Plaza de San Pedro en el Vaticano, fue construida en 1817, siendo papa Pio VII . El obelisco en el centro de la plaza hace de gnomon. En el suelo de dicha plaza existe una línea de granito, que sale del obelisco y que representa el meridiano del lugar, a lo largo de ella hay 7 losas circulares donde se señalan fechas y signos zodiacales.
 |
| Losetas de mármol con fechas y signos del zodiaco |
En esta imagen figura el 21 de marzo y el 23 de septiembre con las fechas de los equinoccios y los signos zodiacales Aries y Libra.
 |
| Meridiana en la Plaza de S. Pedro en Roma |
VII.- En España conocemos tres meridianas, dos de ellas en el Monasterio de El Escorial, una en la Galeria de Paseo, y la otra en la Antecámara del Rey, sala contigua a la anterior y la tercera en el Palacio de Aranjuez.
Las dos meridianas del Monasterio de El Escorial, fueron diseñadas por el matemático y astrónomo Juan Wendlingen (1715-1790) y realizadas por el grabador y escultor Esteban Baumgartner en 1755, según figura en una inscripción en cada una, siendo rey Fernando VI.
Son meridianas más modestas que las italianas, de unos 6 metros de longitud cada una y con el orificio de entrada del rayo de sol a unos 3 metros de altura, sobre un ventanal, son casi idénticas, y están situadas de forma paralela una a otra y a unos 10 metros de distancia. En ellas figuran los meses del año y los signos del zodiaco,
.JPG) |
| Meridiana en el Monasterio de El Escorial. |
La tercera meridiana se encuentra en el Palacio de Aranjuez y fue construida por el mismo matemático y escultor, que las de El Escorial en el año 1747.
VIII.- En París, merece destacar la meridiana de la iglesia de San Sulpicio construida por el astrónomo inglés Henry Sully en 1743 con la particularidad de que la línea en el suelo continua ascendiendo 11 metros por un obelisco en la pared , en los días de equinoccio a mediodía la luz del sol se sitúa sobre un plato oval delante del altar.
VIII.- En París, merece destacar la meridiana de la iglesia de San Sulpicio construida por el astrónomo inglés Henry Sully en 1743 con la particularidad de que la línea en el suelo continua ascendiendo 11 metros por un obelisco en la pared , en los días de equinoccio a mediodía la luz del sol se sitúa sobre un plato oval delante del altar.
Esta iglesia no fue destruida en la Revolución Francesa debido a la importancia de las mediciones y cálculos astronómicos que se hacían con esta meridiana.
 |
| Meridiana de San Sulpicio, París. |
2.- Analemas: Construcción de una meridiana:
Para construir una meridiana: Clavamos una estaca en el suelo (gnomon) o en una pared orientada al sur y cada día siempre a las 12 del mediodía, (hora solar), aunque puede ser a otra hora cualquiera pero siempre a la misma, señalamos el extremo de la sombra de la estaca sobre el suelo o pared.
A lo largo de un año el punto señalado nos describe una figura en forma de 8 o analema.
En su origen la palabra analema viene del griego ἀνάλημμα que significa “pedestal de un reloj de sol” es la curva que describe la posición del Sol en el cielo si todos los días del año se lo observa a la misma hora del día (tiempo civil) y desde el mismo lugar de observación.
El analema forma una curva que suele ser, aproximadamente, una forma de ocho (8) o leminiscata.
Nuevos tipos de analemas:
Después de la invención de la fotografía los analemas adquirieron una nueva dimensión
Si fijamos una cámara de fotos en un trípode e hiciésemos cada día una fotografía al Sol a la misma hora, desde el mismo lugar de observación y durante un año entero obtendríamos una curva con forma de ocho o de lemniscata que es el analema.
 |
| Analema visto desde el hemisferio norte |
El Sol aparecerá en su punto más alto del analema durante el verano y en su punto más bajo durante el invierno. El eje mayor nos indica la declinación del sol.
Los analemas dependiendo de la latitud donde se realice y de la hora del día en que se tome pueden parecer ligeramente diferentes. Vemos unos ejemplos de analemas
 |
El segundo durante 2003, en Atenas, Grecia fotografiado por A. Ayiomamitis.
El tercero, de septbre de 2011 a agosto 2012 en Burgos por Jesús Peláez.
La lazada corta es el reflejo de la mayor velocidad de traslación de la Tierra cuando circula por la sección de su órbita que está más cercana al Sol (y cuyo punto más cercano es el llamado "perihelio") y por la que la gravedad de el Sol ejerce una mayor atracción sobre el planeta.
3.- Hipopede: Matemáticas en el analema:
 El analema se asemeja a dos curvas matemáticas a la Hipopede de Eudoxo y a la Lemniscata de Bernouilli.
El analema se asemeja a dos curvas matemáticas a la Hipopede de Eudoxo y a la Lemniscata de Bernouilli.La hipopede de Eudoxo, o lemniscata esférica, es la intersección de una esfera con un cilindro tangente interior a la esfera, debe su nombre a Eudoxo de Cnido ( 406 a.C. – 355 a.C.)
Tiene una construcción dinámica dada por Eudoxo: La Hipopede es el lugar geométrico de un punto de un círculo máximo inclinado un ángulo alfa sobre el plano del ecuador girando a una velocidad constante alrededor del eje de los polos.
Entonces el punto que recorre ese círculo máximo a la misma velocidad y en sentido contrario a la esfera describe una hipopede.
la ecuación de la hipopede es
Siendo:
r es el radio de la esfera
d distancia del centro de la esfera al eje del cilindro
La lemniscata es una curva en forma de 8 descrita en 1694 por Jakob Bernouilli como el lugar geométrico de los puntos tales que el producto de las distancias a dos focos estas distancias es constante.
Bernoulli la llamó lemniscus, cinta colgante. Su fórmula es
siendo 2a la distancia entre los dos focos.
 |
| Lemniscata de Jakob Bernouilli |
En Gaussianos encontramos esta animación de la hipopede
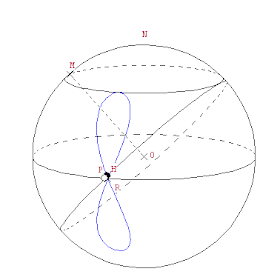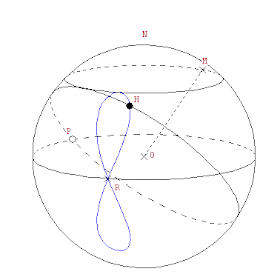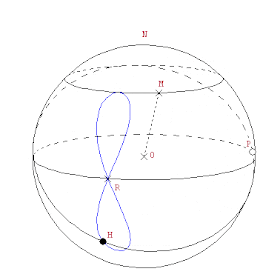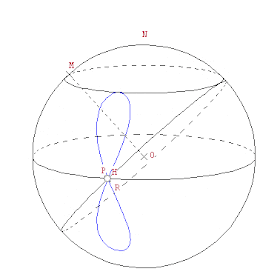
1.- Tenemos una esfera de centro O y que rota a velocidad constante sobre un eje N-S
2.- Sea un punto M que gira sobre un paralelo
3.- Sea P el punto de intersección de los dos círculos máximos perpendiculares a OM y ON
4.- Tomo H, un punto de la circunferencia del círculo máximo perpendicular a OM que se mueve a la misma velocidad pero en sentido inverso que la esfera.
Entonces este punto describe una hipopede.
Como curiosidad hemos encontrado, que en nuestro centro, en el curso de 1º de la ESO grupo D, hay un globo terráqueo en el que podemos ver un analema.
 |
| Globo terráqueo con analema en 1º ESO grupo D |
----------------------------------------------------------------------
Esta entrada participa en la Edición 4.123 del Carnaval de Matemáticas cuyo blog anfitrión en este mes de abril es Eulerianos







Interesantísimo. Enhorabuena
ResponderEliminar